Materi Kurikulum Merdeka Matematika Kelas 7 Bab 1 Bilangan Bulat

Berikut ini Materi Kurikulum Merdeka Matematika Kelas 7 Bab 1 Bilangan Bulat Sesuai dengan Buku Terbitan Kemdikbudristek Tahun 2022.

Pada tahun 2022 penerapan kurikulum merdeka mulai diterapkan pada satuan pendidikan yang mengikuti program Sekolah Penggerak dan Sekolah yang melaksanakan secara mandiri.

Kurikulum merdeka bertujuan memberikan pembaharuan guna meningkatkan kualitas pembelajaran yang telah dilaksanakan dari kurikulum sebelumnya. Misalnya seperti Materi Matematika Kelas 7 Bab 1 Bilangan Bulat ini.

Kurikulum merdeka belajar memberikan kemerdekaan pada sekolah untuk merancang proses serta materi pembelajaran yang relevan dan kontekstual perubahan dalam kurikulum merdeka ini dengan aspek yang berubah dari kurikulum sebelumnya. Contoh Materi Kurikulum Merdeka Matematika Kelas 7 Bab 1 Bilangan Bulat berikut ini sudah Kami Siapkan.

Materi Matematika Kurikulum Merdeka ini disusun berdasarkan struktur Kurikulum merdeka sesuai jenjang SMP/MTs Kelas 7 Bab 1

Materi Matematika Kelas 7 Bab 1 Kurikulum Merdeka

Bilangan Bulat

Bilangan bulat dibedakan menjadi tiga bagian, yaitu:

• Bilangan bulat negatif
• Nol
• Bilangan bulat positif

Masih ingatkah kalian dengan garis bilangan?

Garis bilangan akan membantu kita dalam menyelesaikan persoalan bilangan.

Bilangan bulat negatif letaknya di sebelah kiri.

Bilangan bulat positif letaknya di sebelah kanan.

Perhatikan gambar dibawah ini:

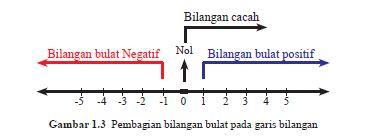
Semakin ke kiri (negatif) semakin kecil nilai angka tersebut.

Semakin ke kanan (positif) semakin besar nilai angka tersebut.

Contoh -1 dan 1, maka lebih besar angka 1.

Contoh lain, -999 dan 1, maka tetap lebih besar 1.

 

Operasi Penjumlahan dan Pengurangan Bilangan Bulat.

Pada bilangan bulat ada beberapa sifat-sifat operasi penjumlahan dan pengurangan.

Sifat tersebut dibagi menjadi 2 yaitu:

• Sifat Komutatif
• Sifat Asosiatif

Mari kita bahas satu persatu.

Sifat Komutatif

Secara umum, jika a dan b adalah bilangan bulat, maka berlaku:

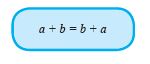
Contohnya :

• 1 + 2 = 2 + 1
• 100 + 10 = 10 + 100
• 9 + 5 = 5 + 9

Cukup mudah kan?

 

Sifat Asosiatif

Secara umum, jika a, b , dan c adalah sebarang bilangan bulat, maka berlaku:

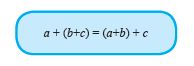
Contoh:

• 120+(30+70) = (120+30) + 70, jumlahnya sama-sama 220.
• 10+(40+20) = (10+40)+20, jumlahnya sama-sama 70.
• 90 + (1+8) = (90+1)+8, jumlahnya sama-sama 99.

 

Selain dua sifat diatas, tahukah kamu bahwa :

• Bilangan genap + bilangan genap  = bilangan genap.
• Bilangan ganjil + bilangan genap = bilangan ganjil.
• Bilangan ganjil + bilangan ganjil = bilangan ganjil.

 

Operasi Perkalian dan Pembagian Bilangan Bulat.

Perkalian Bilangan Bulat

Pada bilangan bulat ada beberapa sifat-sifat operasi perkalian.

Sifat tersebut dibagi menjadi 3 yaitu:

• Sifat Komutatif
• Sifat Asosiatif
• Sifat Distributif

Mari kita bahas satu persatu.

Sifat Komutatif

Secara umum, jika a dan b adalah bilangan bulat, maka berlaku:

a × b = b × a

Contoh:

• 2 × 3 = 3 × 2
• 4 × 5 = 5 × 4
• 199 × 32 = 32 × 199

 

Sifat Asosiatif

Secara umum, jika a, b , dan c adalah sebarang bilangan bulat, maka berlaku:

(a × b)× c = a × (b × c)

Contoh:

• (2 × 3) × 4 = 2 × (3 × 4), sama-sama hasilnya 24.
• (10 × 3) × 4 = 10 × (3 × 4), sama-sama hasilnya 120.
• (2 × 3) × 4 = 2 × (3 × 4), sama-sama hasilnya 24.

 

Sifat Distributif

Secara umum, sifat distributif dalam perkalian dibagi menjadi dua yaitu:

Perkalian terhadap penjumlahan, maka berlaku :

a × (b+c) = (a×b) + (a × c)

Contoh :

• 2 × (5+3) = (2 × 5)  + (2 x 3) = 10 + 6 = 16
• 4 × (10 + 7) = (4 × 10) + (4 × 7) = 40 + 28 = 68
• 9 × (7 + 3) = (9 × 7) + (9 × 3) = 63 + 27 = 90

Perkalian terhadap penjumlahan, maka berlaku :

a × (b-c) = (a×b) – (a × c)

Contoh :

• 2 × (5-3) = (2 × 5)  – (2 x 3) = 10 – 6 = 4
• 4 × (10 – 7) = (4 × 10) – (4 × 7) = 40 – 28 = 12
• 9 × (7 – 3) = (9 × 7) – (9 × 3) = 63 – 27 = 36

Ada tabel yang perlu kalian ingat dalam perkalian bilangan bulat, perhatikan tabel dibawah ini dan hafalkan!

Contoh:

• 2 × 3 = 6 (positif 2 × positif  3= positif 6)
• 2 × (-3) = – 6 (positif 2 × negatif 3 = negatif 6)
• (-2) × 3 = – 6 (negatif 2 × positif 3 = negatif 6)
• (-2) × (-3) = 6 (negatif 2 × negatif 3 = positif 6)

Bagaimana? Mudah kan?

 

Bilangan Prima

Bilangan prima adalah bilangan bulat positif yang hanya memiliki dua faktor, yaitu 1 dan bilangan itu sendiri.

Contoh bilangan prima : 2, 3, 5, 7, 11, 13, 17, 23, dst.

Pembagian Bilangan Bulat.

Secara umum jika a, b, dan c adalah bilangan bulat, maka berlaku:

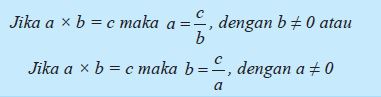
Ingat! Per adalah bagi!

Contoh :

• 2 × 3 = 6, maka 2 = 6 : 3
• 7 × 5 = 35, maka 5 = 35 : 7

 

Urutan Operasi

Dalam mengerjakan soal matematika, ada beberapa urutan yang harus kalian ingat sebagai patokan mana dulu yang harus dikerjakan.

Apabila kalian menemukan soal seperti dibawah ini:

2 + 7 × 5 : 9 – 2 + (5 × 3²) =….

Mana dulu yang harus dikerjakan?

Jangan bingung, perhatikan aturan matematika dibawah ini untuk urutan operasi (yang harus dikerjakan dahulu).

 

Hitung bentuk yang didalam kurung

Contohnya :

• (6 + 2) × 4 = 8 x 4 = 32.
• 7 × (3 +5) = 7 × 8 = 56.

Hitung bentuk eksponen (pangkat)

Contohnya :

• -4 + 3² = -4 + 9 = 5
• 9 + (-4)² = 9 + 16 = 25

Perkalian dan pembagian secara berurutan dari kiri ke kanan

Contohnya :

• 7 × 5 : 35 = 35 : 35 = 1
• 2 + 5 × 9 = 2 + 45 = 47 (ingat perkalian dan pembagian didahulukan daripada penjumlahan dan pengurangan)
• 48 : 2 × 3 = 24 × 3 = 72

Penjumlahan dan pengurangan secara berurutan dari kiri ke kanan

Contohnya :

• 3 – 2 +  5 × 4 = 3 – 2 + 20 = 1 + 20 = 21.
• 3 + 4 : 2 – 5 × 4 = 3 + 2 – 20 = 5 – 20 = (-15).

 

Kelipatan

Sebelum kita mengulas tentang KPK dan FPB, mari kita bahas apa itu kelipatan?

Kelipatan itu hasil perkalian dari angka yang dicari.

Contoh soal :

Tentukan kelipatan 2 yang kurang dari 15!

Untuk menyelesaikan soal diatas kita cukup membuat perkalian 2 saja!

Penyelesaian:

2 x 1 = 2

2 x 2 = 4

2 x 3 = 6

2 x 4 = 8

2 x 5 = 10

2 x 6 = 12

2 x 7 = 14

Maka jawabannya adalah 2,4,6,8,10,12, dan 14.

Karena yang dicari kurang dari 15!

Setelah mengetahui tentang kelipatan, maka kita akan pelajari kelipatan persekutuan.

Kelipatan Persekutuan

Kelipatan persekutuan adalah hasil kelipatan yang sama.

Contoh soal :

Tentukan kelipatan persekutuan dari 1 dan 2!

Penyelesaian:

Kita tinggal membuat tabel perkalian 1 dan 2 saja seperti pada soal sebelumnya!

1 x 1 = 1

1 x 2 = 2

1 x 3 = 3

1 x 4 = 4

1 x 5 = 5

1 x 6 = 6

1 x 7 = 7

1 x 8 = 8

1 x 9 = 9

1 x 10 = 10

Perkalian satu beres, sekarang perkalian dua.

2 x 1 = 2

2 x 2 = 4

2 x 3 = 6

2 x 4 = 8

2 x 5 = 10

2 x 6 = 12

2 x 7 = 14

2 x 8 = 16

2 x 9 = 18

2 x 10 = 20

Nah sekarang tinggal dilihat hasil perkalian, kita tulis yang sama saja.

Jadi kelipatan persekutuan dari 1 dan 2 adalah 2,4,6,8, dan 10.

Gampang kan?

 

Bilangan Prima

Selanjutnya, sebelum masuk ke KPK dan FPB kita harus memahami kembali apa itu bilangan prima.

Karena bilangan prima ini akan sangat digunakan dalam mencari KPK dan FPB.

Bilangan prima adalah bilangan yang hanya bisa dibagi dengan angka itu sendiri.

Contoh bilangan prima adalah 2, 3, 5, 7, 11, 13, 17, dan seterusnya.

 

KPK

KPK adalah singkatan dari Kelipatan Persekutuan Terkecil.

Meski namanya persekutuan terkecil bukan berarti kita cari angka yang kecil loh ya!

Cara Mencari KPK

Dalam mencari KPK dapat menggunakan pohon faktor.

Kita akan membagi angka yang diminta dengan bilangan prima sampai tidak dapat dibagi kembali.

Kemudian melingkari bilangan primanya.

Contoh soal :

Tentukan KPK dari 90 dan 168!

Penyelesaian :

Kita akan gunakan pohon faktor, perhatikan pohon faktor dibawah ini!

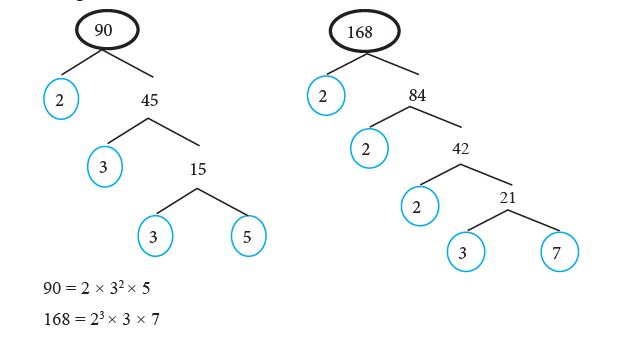
Setelah mengetahui hasilnya, maka untuk menentukan KPK adalah dengan cara :

• Ditulis semua angka utama
• Cari pangkat yang besar

Maka hasilnya :

Berikut penjelasannya:

Sesuai yang Admin jelaskan diatas, kita harus menulis semua angka utama.

Pada hasil pohon faktor 90 diketahui ada angka 2, 3 dan 5

Sedangkan pada hasil pohon faktor 168 diketahui ada angka 2, 3, dan 7.

Kita tulis semua angkanya maka ditemukan angka 2, 3, 5, dan 7.

Kemudian setelah itu kita tentukan pangkat terbesar dari masing-masing angka dan dihitung.

Mudah kan?

 

FPB

FPB adalah singkatan dari Faktor Peresekutuan Terbesar.

Sama seperti ketika mencari KPK, kita dapat menggunakan pohon faktor.

Cara Mencari FPB

Kita akan membagi angka yang diminta dengan bilangan prima sampai tidak dapat dibagi kembali.

Kemudian melingkari bilangan primanya.

Contoh soal :

Tentukan  FPB dari 90 dan 168!

Penyelesaian :

Kita akan gunakan pohon faktor, perhatikan pohon faktor dibawah ini!

Setelah mengetahui hasilnya, maka untuk menentukan FPB adalah dengan cara :

• Ditulis semua angka utama yang sama saja, YANG SAMA SAJA.
• Cari pangkat yang kecil

Maka hasilnya :

2 x 3 = 6

Berikut penjelasannya:

Sesuai yang Admin jelaskan diatas, kita harus menulis semua angka utama yang sama saja.

Pada hasil pohon faktor 90 diketahui ada angka 2, 3 dan 5

Sedangkan pada hasil pohon faktor 168 diketahui ada angka 2, 3, dan 7.

Kita tulis angka yang sama saja maka ditemukan angka 2 dan 3.

Kemudian setelah itu kita tentukan pangkat terkecil dari masing-masing angka dan dihitung.

Demikianlah Materi Mata Pelajaran Matematika Kelas 7 Jenjang SMP/MTs khususnya pada Bab 1 tentang Bilangan Bulat, semoga materi ini dapat membantu para siswa yang akan menggunakannya sebagai bahan belajar dan berlatih.